آزمایش اول-الف) فیلتر پائین گذر
فیلترهای فعال فیلترهایی هستند که برای ساخت آنها از آپ امپ و خازن و مقاومت استفادهشده است . در ساختار این فیلترها سلف هیچ نقشی ندارد .
مزیت اساسی این فیلترها نسبت به فیلترهای پاسیو این هست که در این فیلترها به دلیل بهرهگیری از آپ امپ، امپدانس ورودی خیلی بالا و امپدانس خروجی خیلی پایین است. بنابراین بار اعمالی به خروجی فیلتر تأثیری در عملکرد فیلتر ندارد (برعکس فیلترهای پاسیو که برای بار مشخصی طراحی میشوند) و به دلیل همین خاصیت مهم است که این فیلترها را میتوان بهصورت زنجیرهای اجرا کرد چراکه هر طبقه مستقل عمل کرده و اثر بارگذاری روی طبقهی بعد ندارد و بدین ترتیب میتوان برای نیل به هدف مشخص چند عدد از این فیلترها را سنتز کرد و پشت سر هم وصل کرد.
ادمیتانس های ۱ تا ۵ معرف ادمیتانس های خازنی و مقاومتی هستند.
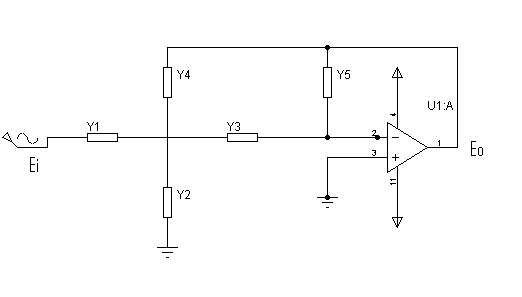
تابع تبدیل مدار فوق بصورت زیر بدست می آید:
\(\frac{E_o(s)}{E_i(s)}=\frac{-Y_1Y_3}{Y_5(Y_1+Y_2+Y_3+Y_4)+Y_3Y_4}\)
با جایگذاری مقاومت بهجای ادمیتانس های ۱و۳ و۴ خازن بهجای ۲و ۵ فیلتر درجه ۲ پایین گذر حاصل خواهد شد.
تابع تبدیل فیلتر بهصورت زیر خواهد بود:
\(\frac{Eo(s)}{Ei(s)}=\frac{\frac{1}{R_1R_3C_2C_5}}{S^2+\frac{1}{C_2}(\frac{1}{R_1}+\frac{1}{R_3}+\frac{1}{R_4)})S+\frac{1}{R_3R_4C_2C_5}}\)
در نهایت تابع تبدیل فیلتر پائین گذر درجه ۲ بصورت زیر بدست می آید:
\(|H(s)|=\frac{H_0 \omega_0^{2}}{{s}^{2}+\alpha\omega_0s+\omega _0^{2}}\\H_0=\frac{R_4}{R_1}\\ \omega_0=\sqrt{\frac{1}{R_3R_4C_2C_5}}\\ \alpha=\sqrt{\frac{C_5}{C_2}}(\sqrt{\frac{R_3}{R_4}}+\sqrt{\frac{R_4}{R_3}}+\sqrt{\frac{R_3R_4}{R_1}})\)
فیلتر پایین گذر را برای دو حالت طراحی می کنیم:
\(\alpha=1,H_0=1,f_0=1Khz\\H_0=\frac{R_4}{R_1}=1 \hspace{15pt} R_1=R_4\\if: C_5=10[nf],C_2=10 C_5=100[nf]\\f_0=1[Khz] \hspace{20pt} \omega_0=2\times{f_0}\times\pi=2000\pi\\2000{\pi}=\sqrt{\frac{1}{R_3 R_4 (10^{-15})}} \hspace{20pt} R_3 R_4=25\times10^6\\ \alpha=\sqrt{\frac{C_5}{C_2}}(\sqrt{\frac{R_3}{R_4}}+\sqrt{\frac{R_4}{R_3}}+\sqrt{\frac{R_3R_4}{R_1}})=1\\ R_3=5.85[K\Omega], R_4=4.27[K\Omega]\)
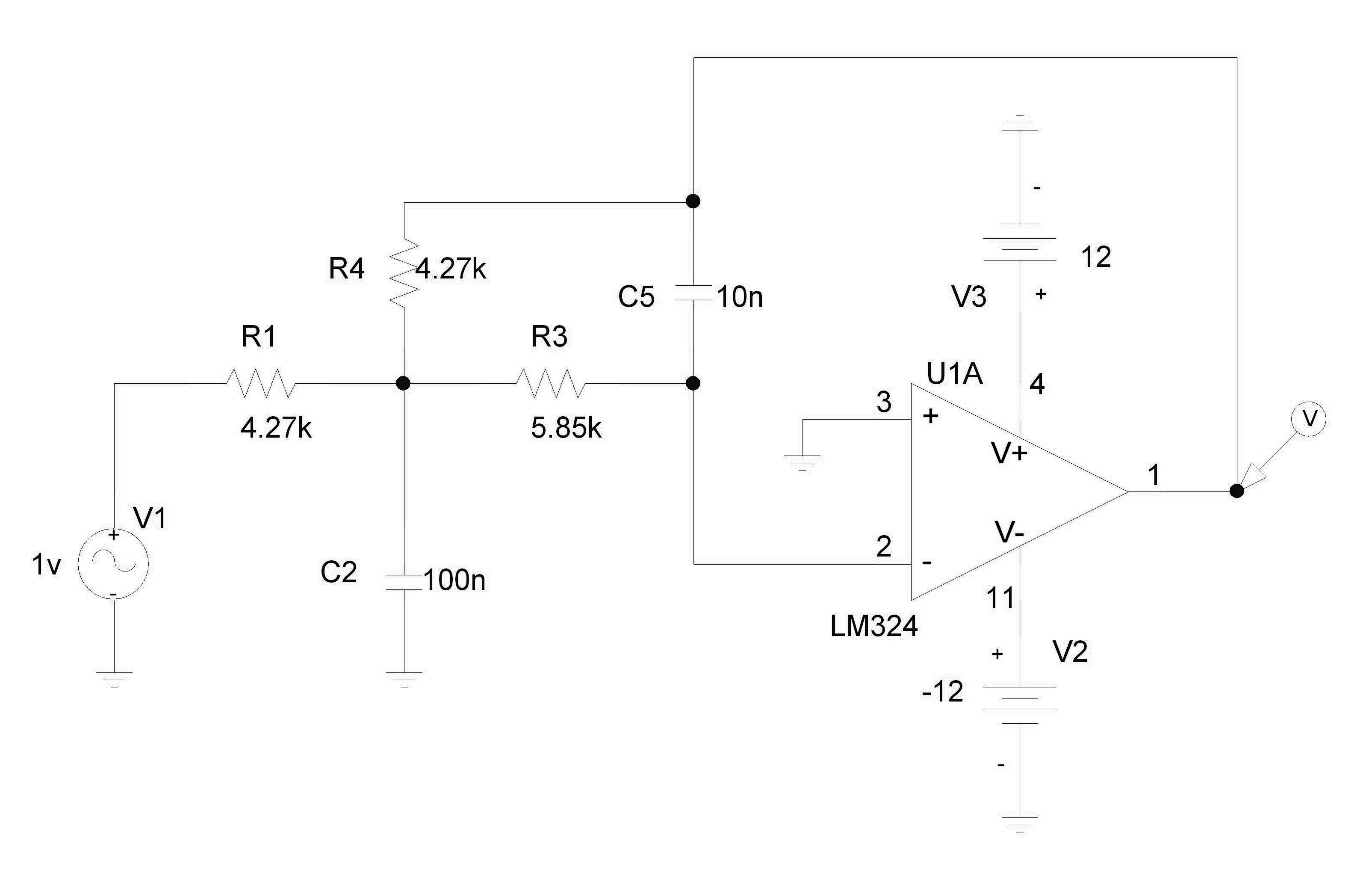
حال با این مقادیر مدار را تکمیل و برای فرکانسهای جدول زیر بهره و اختلاففاز را به دست میآوریم:
| فرکانس | ۱۰۰ | ۲۰۰ | ۳۰۰ | ۴۰۰ | ۵۰۰ | ۶۰۰ | ۷ | ۰۰ | ۸۰۰ | ۹۰ | ۰ | ۹۲ | ۰ | ۹۴۰ | ۹۶۰ | |
| بهره | ۱ | ۱ | ۱ | ۱ | ۱ | ۰٫۹۸۵ | ..۹۸۵ | ۰٫۹۷ | ۰٫۹۵ | ۰٫۹۲ | ۰٫۹ | ۰٫۸۸ | ||||
| اختلاففاز | ۱۸۰ | ۱۷۲ | ۱۶۳ | ۱۴۴ | ۱۴۰ | ۱۳۵ | ۱۲۸ | ۱۱۵ | ۱۰۲ | ۱۰۰ | ۹۵ | ۹۴٫۷ | ||||
| فرکانس | ۹۸۰ | ۱k | ۱۰۲۰ | ۱۰۴۰ | ۱۰۶۰ | ۱۰۸۰ | ۱۱۰۰ | ۱٫۵k | ۲k | ۳k | ۴k | ۵k | ||||
| بهره | ۰٫۸۵ | ۰٫۸۵ | ۰٫۸ | ۰٫۸ | ۰٫۸ | ۰٫۷۵ | ۰٫۷ | ۰٫۵ | ۰٫۴ | ۰٫۲۵ | ۰۲ | ۰٫۱ | ||||
| اختلاففاز | ۸۰ | ۹۰ | ۷۵ | ۷۵ | ۷۰ | ۶۳ | ۶۰ | ۵۵ | ۳۵ | ۲۰ | ۱۲ | ۰ | ||||
نتیجه حاصل از تحلیل اسپایس این مدار به شکل زیر است :
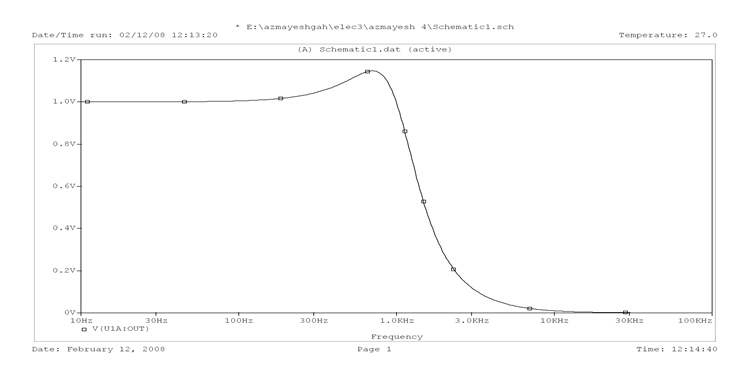
برای بند (ب) که دقیقا مشابه بند (الف) ولی با ضریب کیفیت بالاتر است مقادیر المان های فیلتر را بدست می آوریم:
[math]f_0=1[Khz], H_0=1,\alpha=0.1\\K \geq {\frac{4}{\alpha^2}(1+H_0)}\hspace{15pt}K\geq800\hspace{15pt}K=1000\\C_5=1[nf], C_2=1[uf]\\39.43=\frac{1}{R_3R_4(10^{-15})} \hspace{15pt} R_3 R_4=2.53\times10^7\\ \alpha=0.1=\sqrt{0.001}(2\sqrt{\frac{R_3}{R_4}+\frac{R_4}{R_3}})\\R_3=6.11[K\Omega]\\R_4=4.1[K\Omega][/math]
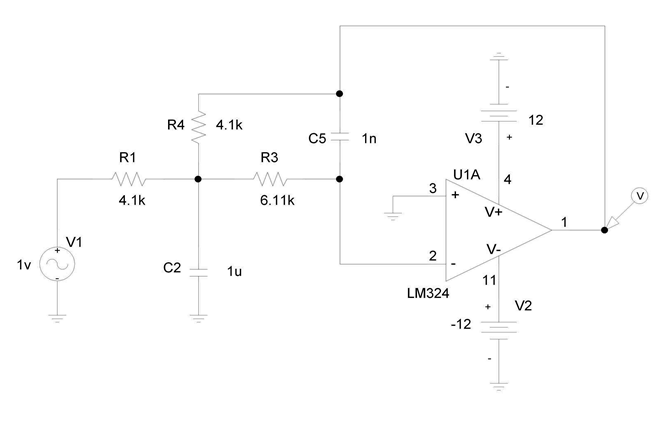
حال با مقادیر جدید دوباره مدار را بسته و جدول را کامل مینماییم:
| فرکانس | ۱۰۰ | ۲۰۰ | ۳۰۰ | ۴۰۰ | ۵۰۰ | ۶۰۰ | ۷۰۰ | ۸۰۰ | ۹۰۰ |
| بهره | ۱ | ۱٫۰۵ | ۱٫۰۸ | ۱٫۱۶ | ۱٫۲۷ | ۱٫۳۷ | ۱٫۷۵ | ۲٫۲۵ | ۳٫۲ |
| اختلاففاز | ۱۸۰ | ۱۸۰ | ۱۸۰ | ۱۸۰ | ۱۷۰ | ۱۶۸ | ۱۶۰ | ۱۵۰ | ۱۳۷ |
| فرکانس | ۹۲۰ | ۹۴۰ | ۹۶۰ | ۹۸۰ | ۱K | ۱۰۲۰ | ۱۰۴۰ | ۱۰۶۰ | ۱۰۸۰ |
| بهره | ۳٫۴ | ۳٫۷ | ۴٫۴ | ۴٫۸ | ۵٫۲ | ۵٫۱ | ۵٫۶ | ۵٫۵ | ۵٫۴ |
| اختلاففاز | ۱۳۷ | ۱۳۰ | ۱۲۳ | ۱۱۳ | ۱۱۳ | ۱۰۹ | ۹۰ | ۹۰ | ۸۰ |
| فرکانس | ۱۱۰۰ | ۱۲۰۰ | ۱۳۰۰ | ۱۴۰۰ | ۱۵۰۰ | ۱۶۰۰ | ۱۶۲۰ | ۲K | ۴K |
| بهره | ۵ | ۲٫۸ | ۱٫۷۵ | ۱٫۲۷ | ۰٫۹۵ | ۰٫۷۵ | ۰٫۷ | ۰٫۳۹ | ۰٫۰۸ |
| اختلاففاز | ۸۰ | ۴۵ | ۲۹ | ۱۵٫۸ | ۱۴ | ۱۲٫۴ | ۱۲ | ۳ | ۰ |
نتایج تحلیل اسپایس:
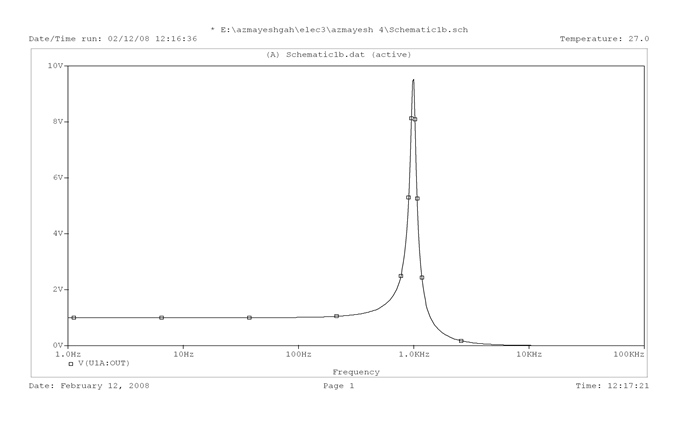
نتیجه:
با افزایش ضریب کیفیت ( Q ) و درنتیجه کاهش مقدار آلفا، مشخصه فیلتر تیز میشود و شیب آن افزایش مییابد و پهنای باند فیلتر کاهش مییابد .

